上回我们说到，卢瑟福实验室的亨利·莫斯莱、德国的詹姆斯·弗朗克和古斯塔夫·赫兹分别通过两个实验验证了玻尔的量化原子模型。

在玻尔的原子模型中有一个量子数叫轨道量子数，也叫主量子数，用字母n表示，那么为什么电子的轨道是不连续的？波尔说，电子绕核运动的角动量是量子化的，它只能是约化普朗克常数h把的整数倍。

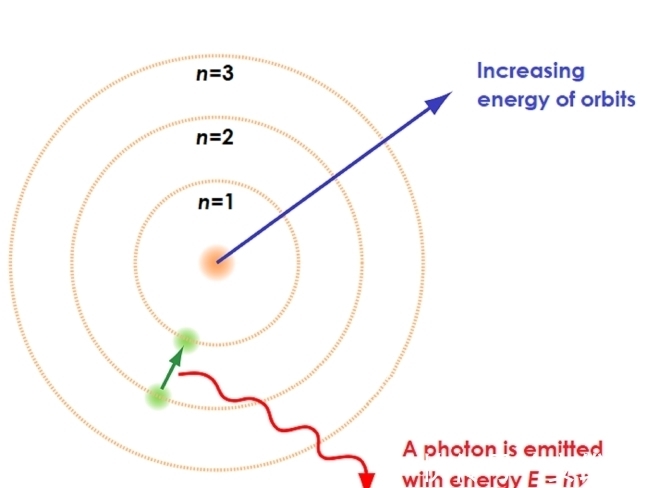
所以电子有第一能级叫基态，有第二、第三、第四等等这些能级，叫激发态。电子吸收足够的能量以后，它就会鬼魅般地跃迁的激发态，至于是第几激发态，就看电子吸收了多少能量。

处在激发态的电子，它会自发地跃迁回更低的能态，并且以电磁波的形式释放出两个能级之间的能量差。

通过以上的假设，玻尔的原子模型解释了氢原子的发射光谱，解释了巴尔末公式为什么有效。关于巴尔末公式，可以回看第十集的视频。

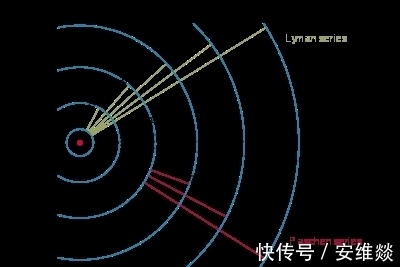
在氢原子的发射光谱中，有一个系列的发射谱线处在可见光波段，称为巴尔末系，分别位于红光、绿光、蓝光、紫光区域，这四条线的产生是电子分别从第三、第四、第五、第六激发态跃迁到第二激发态时，释放出来的，

可是人们后来发现，氢原子光谱的巴尔末系，并不是简单的四条线，如果用更为精确的光谱仪对氢原子的光谱进行分光，再不行，拿个放大镜看氢原子的巴尔末系，就会发现每条光谱线其实并不是一条，而是两条，中间有细小的裂痕。

之所以以前没有发现，是因为这两条线的波长相差非常小，两条线挨得很近，粗略一看以为是一条。这个发现就被称为氢原子光谱的精细结构。

玻尔的原子模型无法解释这个问题，很快，慕尼黑大学的索末菲就给玻尔去了一封信，信中的内容就把这个问题完美地解决了，索末菲给玻尔的原子模型中又添加了一个量子数：叫角量子数，可以叫它轨道形状量子数，这样更容易理解一些。

阿诺德·索末菲，这时48岁，对于一个理论物理学家来说已经过了黄金年龄，不过他所领导的慕尼黑大学物理系很快就要成为量子力学的研究中心，因为他即将迎来两位学生，一个叫泡利，一个叫海森堡。另外两个量子力学的研究中心分别是波恩领导的哥廷根大学的物理系，以及即将要成立的玻尔研究所。这三个地方史称量子力学的金三角。

索末菲这个人一开始是研究数学的，后来转到了理论物理学，他和大数学家希尔伯特、闵可夫斯基是一个地方走出来的同乡，那里数学气氛浓厚，特产就是数学家。

从两个人对索末菲的态度就能看出他有多牛，第一个是爱因斯坦，爱因斯坦这个人一般不会轻易看得上谁，也不会主动去恭维谁，在上学的时候，把闵可夫斯基气的说爱因斯坦是“懒狗”。

不过爱因斯坦在给索末菲的信中就说过，我要是在慕尼黑的话，一定会去找你学习数学物理知识，这时是1908年，爱因斯坦还在专利局工作。你看看，不管是不是真的，爱因斯坦可从来没对别人说过这样的话。

第二个人是泡利，泡利这个人怼天怼地怼空气，他基本上把能怼的人都怼了一遍，人们送他外号：上帝的鞭子。但是只要见到索末菲，不管是在什么场合，泡利都会立刻拘谨起来，对索末菲那是毕恭毕敬。这可能就是人格魅力吧。

回到正题，索末菲从氢原子光谱的精细结构得出了一个关键的信息，线条有分裂，说明这是两个不同能级的电子跃迁到更低的能级产生了，不过裂痕不大，这说明两个电子所在能级的能量相差不大，非常微小。

在玻尔的原子模型中，电子在环形轨道绕着原子核旋转，索末菲就想，电子能不能以椭圆绕着原子核旋转呢？

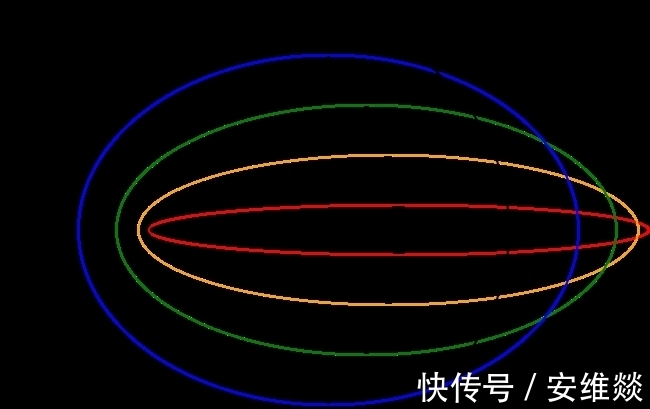
他立刻进行了计算，如果电子以椭圆轨道绕核旋转，那么他的速度就会和环形轨道的电子速度不一样，如果考虑电子运动的相对论效应，那么椭圆轨道的电子就会因为更高的速度而获得更高的质量，因此两个轨道之间就会产生微小的能量差。

这个能量差正好对应两条谱线之间的能量差，如果电子跃迁到了圆形轨道，和跃迁到了椭圆轨道，由于能级不一样，所以释放出来的电磁辐射的波长也有微小的差异。