几个世纪前，数学家们发现，计算某些曲线的性质需要一些看似不可能的东西，当数乘以它们自己时，就会变成负数。

数轴上所有数的平方，都是正数，2^2 = 4，（-2）^2 = 4。数学家们开始称那些熟悉的数字为“实数”，而那些显然不可能的数字则为“虚数”。

虚数以i为单位（例如，（2i）^2 = -4），逐渐成为抽象数学领域的基础。然而，对物理学家来说，实数足以量化现实。从来没有任何仪器返回带有i的读数。

然而，物理学家们可能第一次证明了虚数在某种意义上是真实的。

一群量子理论家设计了一项实验，其结果取决于自然界是否有假想的一面。假设量子力学是正确的（几乎没有人会对这个假设吹毛求疵），该团队的论证本质上保证了复数是我们对物理宇宙描述中不可缺少的一部分。

“这些复数，通常只是一个方便的工具，但它们确实有一些物理意义，”匈牙利科学院核研究所的物理学家塔玛斯·韦特西（Tamás Vértesi）说，“世界就是这样，它真的需要这些复数。

在量子力学中，一个粒子或一组粒子的行为被一个波状实体所封装，称为波函数（ψ）。波函数可以预测测量的可能结果，例如电子的可能位置或动量。所谓的薛定谔方程描述了波函数是如何随时间变化的，这个方程中有虚单位i。

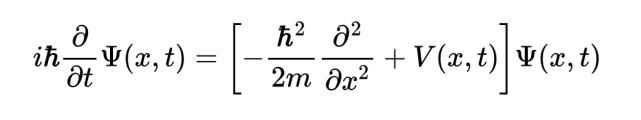物理学家从来没有完全确定这是怎么回事。当薛定谔推导出薛定谔方程时，他希望把i去掉。1926年，他写信给亨德里克·洛伦兹（Hendrik Lorentz），“……令我感到不安的是复数的使用，ψ肯定是一个基本的实函数。”

薛定谔的想法从数学的角度来看当然是合理的，任何复数的性质都可以通过实数的组合加上新的规则来实现，这为量子力学的现实基础打开了数学上的可能性。

事实上，这种解释非常简单，薛定谔几乎立即发现了他认为的“真正的波动方程”，一个令我回避的方程。“又一块沉重的石头从我的心头滚落，”他在给洛伦兹写信后不到一周的时间里给马克斯·普朗克写道。“一切都跟人们想要的一模一样。”

但是，用实数来模拟复杂的量子力学是一项笨拙而抽象的工作，薛定谔认识到他的全实数方程对于日常使用来说太过繁琐。不到一年，他就把波函数用复数表示。

然而，量子力学的真正公式一直在“徘徊”，复数版本只是一个选择。例如，在2008年和2009年的一项研究表明，在没有i的情况下，可以完美地预测著名的量子物理实验——贝尔测试的结果。

今年，研究发现，那些早期的贝尔测试提案并没有走得太远，不足以推翻量子物理学的实数版本。它提出了一个更复杂的贝尔实验，似乎需要复数。

早期的研究让人们得出这样的结论：在量子理论中，复数只是为了方便计算和表示，而不是必需的，”现在物理学家证明这个结论是错误的。

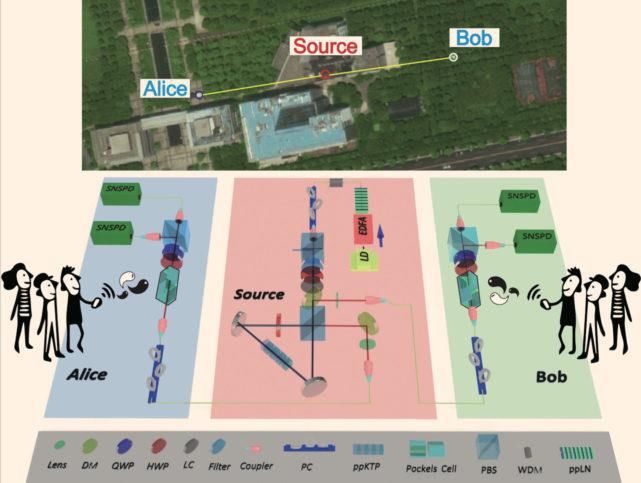
贝尔实验表明，相距遥远的一对粒子可以在单一的“纠缠”状态下共享信息。例如，如果地球上的的一枚硬币和火星上的一枚硬币纠缠在一起，那么反复抛硬币就会发现，只要有一枚硬币是正面朝上的，那么它远处的同伴就会奇怪地露出反面。同样，在标准的贝尔测试实验中，纠缠粒子被发送给两位物理学家，昵称为爱丽丝和鲍勃。他们测量这些粒子，通过比较测量结果，发现这些结果以一种无法解释的方式相互关联，除非这些粒子之间共享信息。

升级后的实验增加了粒子对的第二个来源。一对送给爱丽丝和鲍勃。第二组，来自另一个地方，给了鲍勃和第三方，查理。在复数量子力学中，爱丽丝和查理接收到的粒子不需要相互纠缠。

然而，任何实数描述都无法复制这三位物理学家将要测量的关联模式。这篇新论文表明，将系统视为实系统需要引入额外的信息，这些信息通常位于波函数的虚部。爱丽丝、鲍勃和查理的粒子必须共享这一信息，才能重现标准量子力学中相同的相关性。而适应这种共享的唯一方法是它们所有的粒子相互纠缠。

在之前的贝尔测试中，爱丽丝和鲍勃的电子来自一个单一的来源，所以他们必须携带的额外信息在实数描述中不是问题。但在双源贝尔测试中，爱丽丝和查理的粒子来自独立的源，虚构的三方纠缠在物理上没有意义。

即使没有爱丽丝、鲍勃和查理来实际执行这篇新论文设想的实验，大多数研究人员也非常自信，认为标准量子力学是正确的，因此该实验将找到预期的相关性。如果是这样的话，那么仅靠实数字并不能完全描述自然。